Ariel University
Course name: Deep learning and natural language processing
Course number: 7061510-1
Lecturer: Dr. Amos Azaria
Edited by: Moshe Hanukoglu
Date: First Semester 2018-2019
Convolutional Neural Networks (CNN)
Introduction
Until now, we have dealt with fully-connected networks, meaning that each neuron is connected to each neuron in the next layer. Due to this structure of the network it is necessary to create a lot of weights and creating a lot of weights makes it very difficult calculations
In this chapter we will focus on a network of Convolational Neural Networks (CNN). This network can learn the right features to look for in data. This network is very useful in image processing.
Description of the network structure
Each layer in the network has a kernel that consists of one or more matrixes. Each matrix is a filter for another feature in the input for that layer.
Each cell in each matrices is the weight the network will learn (similar to weights in fully-connected) to get the correct result at the end.
The grid receives a matrix in the input, and moves the kernel over the entire matrix from the upper left corner to the lower right corner. In each shift, it calculates the sum of the kernel's product values with the matrix values where the kernel is.
For example:
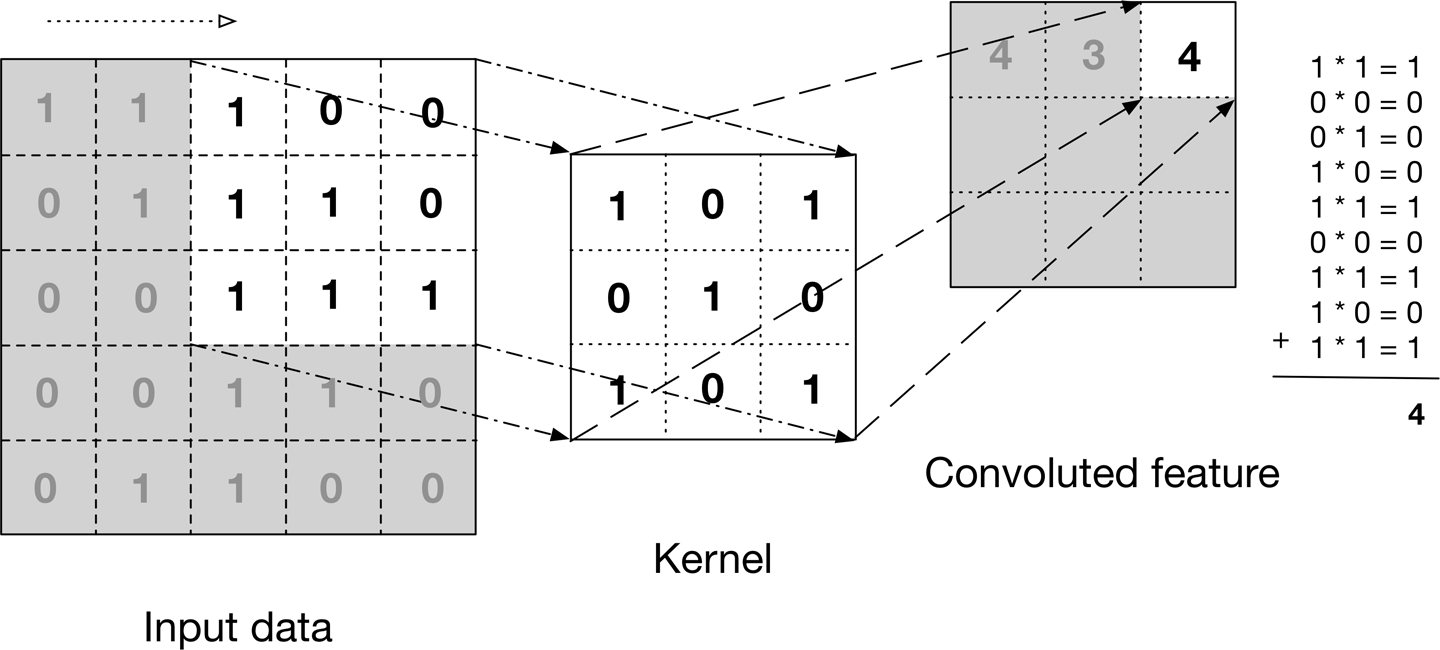
When the numbers in each matrix can be any number.
In the calculation above there is one input matrix (the big matrix) and the kernel is also built from one matrix.
There may be several matrices in the kernel, in which case we will perform the action described above for each of the kernel matrices.
Note: It is not necessary for the kernel to move in one square at a time; it can move in a few squares.
Sometimes a bias is added to each of the cells in each of the matrices or the matrices are inserted into the activation function.
Representing the size of the kernel
When we want to represent the size of the kernel we will write it as follows [Height, width, depth, number of filters].
The depth parameter can not be decided by the programmer but is determined by the dimension of the input.
In the case shown above the representation shall be [3,3,1,1]
In the case shown below the representation will be [3,3,3,1]
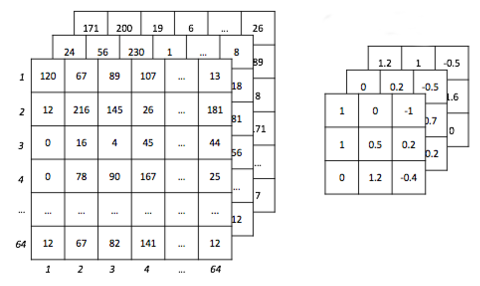
We can determine the stride of the sliding window for each dimension of input that is, the sliding window can skip on two cell in each move.
Padding
Increase the matrix to the size you want. This helps the output matrix to be larger (helps in some cases).
- Same - want to pad
- Valid - do not want to pad
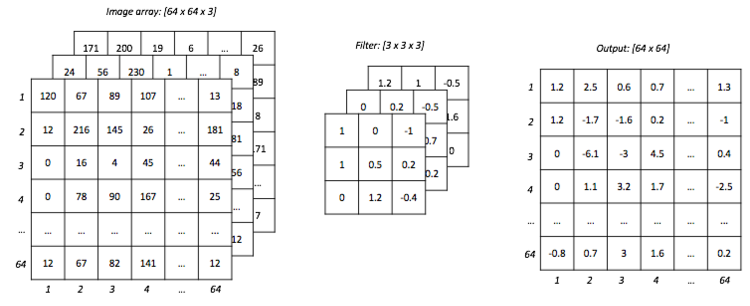
n-D Convolution Weights
In practice, the input to the convolution layer is many times 3-dimensions. In that case, in every kernel group, each kernel multiplies a different dimension and the results are summed up.
Max-Pooling
This method reduces the dimensions of the input matrix. This method is also used as an activation function and it also reduces the chances of over-fitting.
The way it works is to divide the matrix into equal parts and take the maximum from each part.
For example:
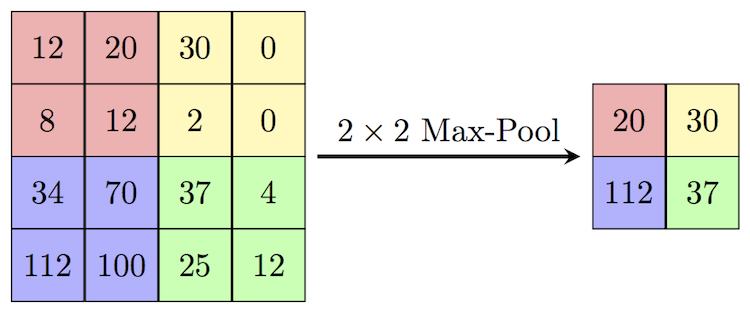
Dropout (Regularization)
Given a network in the form of a fully-connected with weights on the arches, then in every few rounds determine the output of some neurons 0, after a few more rounds decide that the output of some other neurons is 0 and continue.
When the other neurons whose output is not equal to 0 receive a higher weight (for example, their weights are multiplied by only 2 for those rounds).
There are a number of explanations why layers help dorpout:
- Random "shutdown" of neurons makes it difficult for the network to reach overfitting, because each time it sees the information flow from the input in a different way.
- Requires the model to train all the weights of all neurons (not to reach 0) because each time only some of the neurons work and therefore they should be used as backup for neurons that do not work. And this may improve overall performance.
- When we turn off a part of neurons is similar to training of models in different forms which gives a more general model
Identifying Numbers Handwritten By CNN
Network for MNIST handwritten number recognition.
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_datamnist = input_data.read_data_sets("MNIST_data/", one_hot=True)x = tf.placeholder(tf.float32, shape=[None, 784])
y_ = tf.placeholder(tf.float32, shape=[None, 10])
Create an array with dimensions [5, 5, 1, 32] and fill it with numbers about 0 with a standard deviation of 0.1.
That is, in the kernel has 32 filters with size 5 x 5 x 1.
W_conv1 = tf.Variable(tf.truncated_normal([5, 5, 1, 32], stddev=0.1))
b_conv1 = tf.Variable(tf.constant(0.1, shape=[32]))
Reshape the array of x from a size of None x 784 to size of None x 28 x 28 x 1. If we had RGB image, we would have 3 channels that is, None x 28 x 28 x 3.
x_image = tf.reshape(x, [-1,28,28,1])
Now, run the convolution layer with the images, the kernel, and an array that describe the stride of the sliding window of weights for each dimension of the input and we want padding.
After the ReLU, running max_pool the max_pool gets the output of the convolution layer, previous layer, the size of the window for each dimension of the input tensor as a list, the stride of the sliding window for each dimension of the input tensor as a list and we want padding.
h_conv1 = tf.nn.relu(tf.nn.conv2d(x_image, W_conv1, strides=[1, 1, 1, 1], padding='SAME') + b_conv1)
h_pool1 = tf.nn.max_pool(h_conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
W_conv2 = tf.Variable(tf.truncated_normal([5, 5, 32, 64], stddev=0.1))
b_conv2 = tf.Variable(tf.constant(0.1, shape=[64]))h_conv2 = tf.nn.relu(tf.nn.conv2d(h_pool1, W_conv2, strides=[1, 1, 1, 1], padding='SAME') + b_conv2)
h_pool2 = tf.nn.max_pool(h_conv2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
W_fc1 = tf.Variable(tf.truncated_normal([7 * 7 * 64, 1024], stddev=0.1))
b_fc1 = tf.Variable(tf.constant(0.1, shape=[1024]))h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)W_fc2 = tf.Variable(tf.truncated_normal([1024, 10], stddev=0.1))
b_fc2 = tf.Variable(tf.constant(0.1, shape=[10]))y_conv=tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y_conv), reduction_indices=[1]))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy) #uses moving averages momentum
correct_prediction = tf.equal(tf.argmax(y_conv,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())for i in range(10000):
batch = mnist.train.next_batch(50)
if i%100 == 0:
train_accuracy = accuracy.eval(feed_dict={x:batch[0], y_: batch[1], keep_prob: 1.0})
print("step %d, training accuracy %g"%(i, train_accuracy))
train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})print("test accuracy %g"%accuracy.eval(feed_dict={x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))
The structure of the network is in this order:
Reshape the x to [None, 28,28,1].
- Convolution layer (ReLU), kernel [5, 5, 1, 32], input [None,28,28,1].
- Max Pool layer, input from convolution layer.
- Convolution layer (ReLU), kernel [5, 5, 32, 64], input from Max Pool layer.
- Max Pool layer, input from convolution layer.
Reshape the x to [None, 7764]
- Fully-connected layer (ReLU), 1024 neurons, input from Max Pool layer.
- Dropout layer, input from the fully-connected layer.
- Softmax layer, input from the dropout layer.
tf.layer
Instead of manually stating all the Ws bs etc., we can use contrib.layers:
- Convolution layer
tf.layers.conv2d(inputs = conv1, filters = 32, kernel_size = [4,4], strides = [1,1], padding = 'VALID', activation = tf.nn.relu)
- Fully-connected layer
tf.layers.dense(last_layer, units = 10, activation=tf.nn.relu)