Ariel University
Course name: Deep learning and natural language processing
Course number: 7061510-1
Lecturer: Dr. Amos Azaria
Edited by: Moshe Hanukoglu
Date: First Semester 2018-2019
Multilayer Perceptron
Introduction
We will define some definitions before we begin to engage in this subject in depth.
Perceptron
This is a small unit that has inputs, a function to process the inputs, and an output.
This unit looks like this:
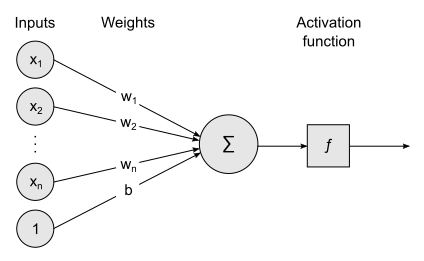
Part One: Inputs
Each input has weight. We denote the input $i$ as $x_i$ and the weight of $x_i$ as $w_i$. Each input can be 0 or 1.
Sometimes we add one input called bais and its value will always be 1 and its weight will be marked as $b$.
Part Two: Activation function
Multiply all its weight and input and sum everything, that is $\sum_{i = 1}^{n} {w_ix_i}$ and then put the result into a given function. We will talk about the types of functions below.
Part Three: Output
The output of the unit will be the output given by the function. If this unit is connected to other units (as we will see below) then each of the other units connected to it will receive the output of this unit.
Multilayer Perceptron (Neural Network, NN)
is a structure composed of several perceptron that are connected to each other.
This structure looks like this:
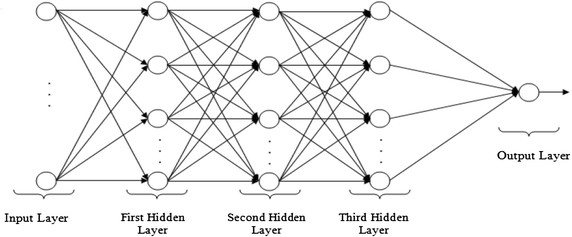
When each line of perceptron is called a layer, the first layer is called the input layer, the last layer is called the output layer and the other layers are called hidden layers.
Note: In cases where all neurons do the same, we initialize the weights to small random values so that we do not get the same result in all neurons.
Fully-connected
Is a multilayer perceptron that each perceptron level $i$ is connected to each perceptron at the $i + 1$ level, as in the image above.
Feedforward and backpropagation
This method is to find the right sounds on the bow so that the output is correct.
In linear / logistic regression we looked for the right weights to get the right result when we put in new input, here, too, we want to find the right weights.
The difference between the cases is the difficulty in finding the weights, because in linear / logistic regression one group of weights was found that was almost independent of them. Now in neural network you have to find all the weights that are on the arches between the layers and any change in weight affects all the weights that are connected to it.
To expand knowledge link
Why use Multilayer Perceptron?
Until now, all learning was based on features we knew about data in advance and we taught the model to predict things based solely on the features we knew in advance. And we were able to learn only about these qualities.
The use of multilayer perceptron comes to help the model learn about more featurs and also more abstract connections.
Activation Function
An activation function is one function of a set of functions into which we insert the sum $\sum_{i = 1}^{n} {w_ix_i}$ and it gives some value other than the sum.
The question is why not stay with the amount we received as it is and output it but put it into the activation function?
If we do not use the activation function, but each neuron exits the sum $\sum_{i = 1}^{n} {w_ix_i}$ then if we analyze and open parentheses in the calculation of the final output we find that the final output (for each neuron in the output layer) is from the form $x_i*(Linear\ combination\ of\ weights)$
This means that the equation is exactly the same equation as linear regression, and we want to build the neural network so as not to reach the same answer again as linear regression but to another answer.
Therefore, in the output of each neuron we perform an activation function in order to "break" the linearity.
There are many types of activation functions (as can be seen in the link).
We'll display three common functions:
- $ReLU(x) = \left\{\begin{array}{ll}x & x > 0 \\0 & otherwise\end{array}\right.$
- $Leaky ReLU(\alpha,x) = \left\{\begin{array}{ll}x & x > 0 \\\alpha x & otherwise\end{array}\right.$
- $ELU(\alpha,x) = \left\{\begin{array}{ll}x & x > 0 \\\alpha(e^x-1) & otherwise\end{array} \right.$
The $Leaky ReLU(\alpha,x)$ and $ELU(\alpha,x)$ prevent dead neurons because negative values also get value. Meaning that it will be gradient for any value and we can continue to calculate the values of the neuron.
MultiLayer Perceptron For Identifying Distance
Data pairs of numbers and each pair given a label.
You have to build a model that could give the right label to a couple of numbers that he had not seen before.
import tensorflow as tf
import numpy as npfeatures = 2
hidden_layer_nodes = 10
x = tf.placeholder(tf.float32, [None, features])
y_ = tf.placeholder(tf.float32, [None, 1])
Construction of the first layer.
The truncated_normal function randomly initializes the weights with a normal distribution and dependence on stddev.
We give a positive bias to prevent dead neurons, because once a neuron reaches 0, it will always remain with 0 as a result of the ReLU.
W1 = tf.Variable(tf.truncated_normal([features,hidden_layer_nodes], stddev=0.1))
b1 = tf.Variable(tf.constant(0.1, shape=[hidden_layer_nodes]))
z1 = tf.add(tf.matmul(x,W1),b1)
a1 = tf.nn.relu(z1)
W2 = tf.Variable(tf.truncated_normal([hidden_layer_nodes,1], stddev=0.1))
b2 = tf.Variable(0.)
z2 = tf.matmul(a1,W2) + b2
y = tf.nn.sigmoid(z2)
loss = tf.reduce_mean(-(y_ * tf.log(y) + (1 - y_) * tf.log(1 - y)))
update = tf.train.GradientDescentOptimizer(0.0001).minimize(loss)data_x = np.array([[2,32], [25,1.2], [5,25.2], [23,2], [56,8.5], [60,60], [3,3], [46,53], [3.5,2]])
data_y = np.array([[1], [1], [1], [1], [1], [0], [0], [0], [0]])sess = tf.Session()
sess.run(tf.global_variables_initializer())
for i in range(0,50000):
sess.run(update, feed_dict = {x:data_x, y_:data_y})
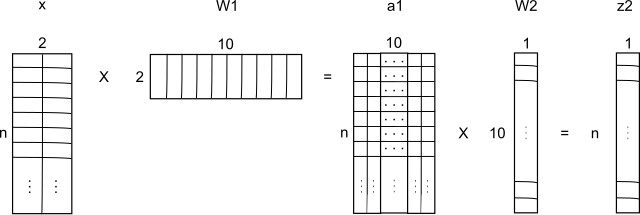
The structure of this network is 2 neurons in the input layer, 10 neurons in the middle layer (hidden layer) and one neuron in the output layer.
We will present the structure of the network in the form of matrices:
The addition of the values of b we have not shown, this is only general evidence.
print('prediction: ', y.eval(session=sess, feed_dict = {x:[[13,12], [0,33], [40,3], [1,1], [50,50]]}))
Predicting Handwritten Numbers
In order for us to begin the prediction we need to teach our model on an existing dataset and for each data point there is a label of the actual number it represents.
Dataset's very familiar handwritten numbers is MNIST, a dataset that contains 60,000 samples with labels.
Build the NN model and use SoftMax to decide which digit.
Source: link
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import matplotlib.pyplot as plt
import numpy as np# Dounload the MNIST dataset and save it in MNIST_data folder.
# one_hot is One_hot means that for each data point we create an array the size of the classes, fill the array with '0',
# and only in the class whose data point belongs to it we will denote '1'.
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)(hidden1_size, hidden2_size) = (100, 50)
x = tf.placeholder(tf.float32, [None, 784])
y_ = tf.placeholder(tf.float32, [None, 10])W1 = tf.Variable(tf.truncated_normal([784, hidden1_size], stddev=0.1))
b1 = tf.Variable(tf.constant(0.1, shape=[hidden1_size]))
z1 = tf.nn.relu(tf.matmul(x,W1) + b1)W2 = tf.Variable(tf.truncated_normal([hidden1_size, hidden2_size], stddev=0.1))
b2 = tf.Variable(tf.constant(0.1, shape=[hidden2_size]))
z2 = tf.nn.relu(tf.matmul(z1,W2) + b2)W3 = tf.Variable(tf.truncated_normal([hidden2_size, 10], stddev=0.1))
b3 = tf.Variable(tf.constant(0.1, shape=[10]))y = tf.nn.softmax(tf.matmul(z2, W3) + b3)
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(cross_entropy)sess = tf.Session()
sess.run(tf.global_variables_initializer())correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))iteration_axis = np.array([])
accuracy_axis = np.array([])for i in range (500):
for _ in range(1000):
batch_xs, batch_ys = mnist.train.next_batch(100)
sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
iteration_axis = np.append(iteration_axis, [i], axis=0)
accuracy_axis = np.append(accuracy_axis, [sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels})], axis=0)
print("Iteration: ",i, " Accuracy:", sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))
The structure of this network is 784 neurons in the input layer, 100 neurons in the first hidden layer, 50 neurons in the second hidden layer and 10 neuron in the output layer. And finally put the outputs to softmax.
plt.plot(iteration_axis, accuracy_axis)
plt.show()
Resolving Errors
If train error is too high:
- Error in code
- Extend the training time
- Add more layers or more features
- Change the $\alpha$ or the initial values of the weights
- Change the activation function (eg: SGD, RMSProp, Adagrad, Adam)
If test error is too high (but train-error is ok):
- Add more data to dataset
- Use early stopping
- Use regularization
- Dropout
- Ridge/LASSO